Laboratorio N°12 y 13

''Año de la lucha contra la corrupción y la impunidad".

Laboratorio N° 12

Circuitos Digitales

Matriz de Leds

Alumno(s)		Nota
- Ccora Mamani, Jhair Antony
- Neira Mamani, Pool Deivis
- Flores Zenteno, Hairo Alexis
Grupo
Ciclo  2C5	Electrónica y Automatización – Circuitos Digitales
Fecha de entrega

       I.      CAPACIDAD TERMINAL

●       Identificar las aplicaciones de la Electrónica Digital.

●       Describir el funcionamiento de las unidades y dispositivos de almacenamiento de información.

●       Implementar circuitos de lógica combinacional y secuencial.

     II.      COMPETENCIA ESPECIFICA DE LA SESION

●       Implementación de Registros en Serie

●       Contador en Anillo con Registro serie

●       Identificación de terminales y prueba de Matriz de Leds

CONTENIDOS A TRATAR

●       Registros Series

●       Contador en Anillo

●       Matriz de Leds.

   IV.      RESULTADOS

●       Diseñan sistemas eléctricos y los implementan gestionando eficazmente los recursos materiales y humanos a su cargo.

    V.      MATERIALES Y EQUIPO

●       Entrenador para Circuitos Lógicos

●       PC con Software de simulación.

●       Guía de Laboratorio. El trabajo se desarrolla de manera GRUPAL.

   VI.      REPASO DEL LABORATORIO ANTERIOR

●       Contadores especiales y Reductores de Frecuencia.

 VII.      FUNDAMENTO TEÓRICO

●       Revise los siguientes enlaces:

●       REGISTROS EN SERIE

http://hispavila.com/total/3ds/tutores/ls192.htm

●       CONTADORES EN ANILLO:

 https://unicrom.com/multivibrador-monostable-con-temporizador-555/

TEORIA DE MATRIZ DE LEDS:

Matriz de Leds

• Una matriz de leds es un display formado por multiples leds, en una distribucion rectangular. Existen distintos tamaños, el mas abitual es el de 8x8. Estos se dividen en filas y columnas claramente se tiene que ver con anterioridad la posicion de los Anodos y Catodos para realizar cualquier trabajo.

Contadores en Anillo

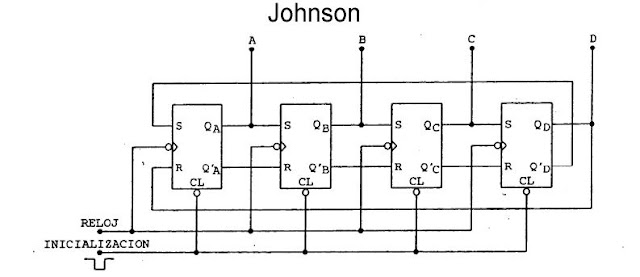
• Contador en anillo. Constituye un registro de desplazamiento en el cual la entrada del 1er Flip-Flops esta condicionada por la salida del ultimo, constituyendo así una cadena cerrada.
• La información introducida inicialmente circula permanentemente por los biestables sin perderse.
• si al comienzo un biestable es puesto en "1" y el resto en "0" (lo cual se logra con las entradas asincrónicas Set y Reset de cada Flip-Flop).
• En contador en anillo funciona pasándose de Flip- Flop a Flip-Flop un unico bit. Esto quiere decir que, en cualquier instante del proceso de conteo, solo un Flip-Flop tiene su salida Q=1. Esto provoca que el contador en anillo sea el contador mas fácil de decodificar.De hecho, sabiendo que el Flip-Flop esta a uno, conocemos en que estado se encuentra el contador.

Implementacion de Contador Jhonson,(SOFTWARE PROTEUS):

Video Tutorial Explicando lo Realizado en Laboratorio:

https://www.youtube.com/watch?v=s8Wr7AkmHqw&feature=youtu.be

Observaciones y Conclusiones:

• Faltaba Cables para la realización del Laboratorio.
• A realizar una implementación de registros en serie.
• A realizar y entender el comportamiento de un contador en anillo con registro serie.
• A identificar de terminales y prueba de Matriz de leds.
• Describir el funcionamiento de las unidades y dispositivos de almacenamiento de información.
• Implementar circuitos de lógica combinacional y secuencial.

¿Que he aprendido de esta experiencia?

• Implementar registros en serie de forma practica y en simulación.
• Armados de un Contador en Anillo con Registro serie.
• Logre identificar de terminales y prueba de Matriz de leds.

Laboratorio N°11

Laboratorio N°10

''Año de la lucha contra la corrupción y la impunidad".

Laboratorio N° 10

Circuitos Digitales

Contador Jhonson Y Divisor de  Frecuencia.

Alumno(s)		Nota
-Ccora Mamani, Jhair Antony
-
-Neira Mamani, Pool Deivis
Grupo
Ciclo  2C5	Electrónica y Automatización – Circuitos Digitales
Fecha de entrega

Contador Johnson

El contador Johnson o contador conmutado en cola es una variación del contador en anillo que duplica el número de estados codificados, sin sacrificar su velocidad. Lo que si complica algo es la decodificación del estado.

 Tabla de como trabaja el contador según los pulsos.

 Divisor de frecuencia

El JK flip-flop es un divisor-por-dos, porque el cambia de estado cada vez que un pulso activo alcanza su entrada; esto es, el primer pulso SETS (pone) al JK en lógica 1 (nivel H), y el segundo pulso lo RESETS (devuelve) a lógica 0 (nivel L).

Así, se requieren dos pulsos de entrada para proporcionar un pulso de salida. Las variables A y B de la figura 20 fueron escogidas para ilustrar esta división. Podemos considerar que A es la entrada para JK, y que B es su salida. Observemos que, por cada segmento igual de tiempo, sólo hay en B una cantidad de pulsos igual a la mitad de los pulsos presentes en A. Consecuentemente, la frecuencia de B es la mitad de la de A.

Si dos JK's son conectados en cascada (con la salida del primero manejando la entrada del segundo), el resultado será un circuito divisor-por-cuatro, porque la división por 2 del primer JK es dividida nuevamente por 2 en el segundo JK. 

Contadores digitales Cuando se conectan en cascada flip-flops JK, el resultado es una división por 2n (2 a la segunda potencia n), donde "n" es el número de etapas en cascada. así, tres JK's en cascada dividirán por 8, porque 2(3) = 8. Ver en la figura 21 el diagrama de tiempos para un divisor por 8. 2n significa que se debe multiplicar entre sí la base 2 un número "n" de veces, para obtener la cantidad que representa.

Es bastante fácil hacer divisiones cuyo divisor sea un número entero potencia de 2. Es poco más complicado si se desea dividir por diez, por ejemplo, porque tres JK's dividen por 8 y un cuarto JK's dividiría por 16. Es necesario, entonces, usar cuatro JK's y monitorizar la cantidad acumulada.

Cuando la cantidad alcance diez, es necesario proveer un pulso de salida y reset todos los JK's para que arranquen de nuevo en cero. Para hacer esta división por 10 se consiguen circuitos integrados, conocidos como DIVISOR POR DECADAS, pero se puede implementar como aparece en el diagrama lógico de la figura 22.

Divisores de frecuencia digital Un circuito divisor-por-diez podrá, en efecto, contar de o a 9. En la siguiente imagen, aparecen representados los números binarios con su equivalente decimal al frente (observemos que, la acción descrita por esta tabla, implica que cada etapa del circuito lógico cambie de estado solamente cuando la etapa precedente pasa a lógica 1 a lógica 0, es decir, únicamente cuando "caiga el pulso").

Las letras A, B, C y D se refieren a los JK's del diagrama en bloques (block diagram). Los JK's están numerados de derecha a izquierda de tal forma que sus estados, cuando se tabulen, aparezcan en el orden convencional establecido para los números binarios.

Contadores digitales Cuando todos los flip-flops están en el estado lógico 0, ellos tienen el número CERO. Cuando A está en lógica 1, C en lógica 0, y D está en lógica 1, los flip-flops tienen número 5. El razonamiento anterior se puede aplicar para cualquier número, entre 0 y 15.

Para dividir por 10, es necesario detectar el número 9, y aprovechar la caída de su pulso para reponer todas las etapas del circuito. Para este número, A es lógica 1, B es lógica 0, C es lógica 0 y D es lógica 1, datos que escritos en forma de expresión Booleana nos da lo siguiente:

E = A no-B no-C D, que se lee "E es igual a A and no-B and no-C and D"(el and significa la conjunción y en español, pero se ha dejado su equivalente inglés para visualizar mejor la clase de compuerta electrónica necesaria para implementar esta expresión del álgebra do boole: la AND.

Como se muestra en la parte superior de la siguiente figura, se usa una compuerta NAND de cuatro entradas para implementar esta función. Observemos que los JK flip-flops proporcionan directamente las salidas para No-B y NO-C. La salida B es lógica 1 cuando B no es lógica 1. Toda vez que el número 9 es detectado, la salida de la compuerta AND se pasa a lógica 1. Este nivel lógico sirve como señal de salida para el circuito divisor-por-diez, y como señal de reset para todos los JK.

Observemos que se ha incluido un circuito monoestable one-shot (OS) entre la salida y la línea de entrada reset para los flip-flops. El monoestable genera un puslo de logitud definida cada vez que el DATA PULSE cae (cada que el pulso propio del divisor cambia de nivel alto a nivel bajo), de ancho suficiente para dar tiempo a que todos los flip-flops se repongan (recordemos que está de por medio el tiempo de propagación, que, aunque es de unos 20 nanosegundos es TTL, es digno de tener en cuenta). Este mismo principio de REALIMENTACION (feedback) es usado para generarla salida y el reset de cualquier otro divisor.

. OBSERVACIONES

• Es preferible que antes de hacer la implementación del circuito, hacer su respectiva simulación para así conocer el funcionamiento y evitar errores en cuanto a conexiones.
• Es importante primero revisar el funcionamiento de cada flip-flop, ya que de encontrarse alterado o con falla, perjudicará al funcionamiento correcto del circuito.

• En el laboratorio se usó un generador de cloc, el cual  su pin CT debe de estar conectado a tierra necesariamente para el correcto funcionamiento del circuito.
• Antes de proceder al armado revisar la continuidad de los cables para evitar errores futuros.

. CONCLUSIONES

• Se concluye que se conoció el funcionamiento del contador Johnson, así como el respectivo análisis de su tabla de verdad.

• Se concluye que con n flip-flops, un contador Johnson es capaz de codificar 2n estados, y aunque la decodificación se complica, la velocidad de conteo es igual a la del contador en anillo.

• Concluimos que se llama divisor de frecuencia a un dispositivo electrónico que divide la frecuencia de entrada en una relación casi siempre entera o racional, la forma de la señal de salida puede ser simétrica o asimétrica. La señal de entrada frecuentemente tiene forma de una onda cuadrada pero también puede ser sinusoidal o de otras formas.

• Concluimos que a partir de una adecuada conexión de varios flip-flop, se puede obtener un circuito digital divisor de frecuencia, los cuales son dos tipos de divisores de frecuencia, de manera par e impar, la cual depende de las conexiones entre los flip-flops.

• En conclusión, en un divisor de frecuencia impar, el periodo varía de manera impar, es decir, cierto tiempo este prendido y un durante un tiempo diferente permaneces apagado.

• Se concluye que el divisor de frecuencia par, consecutivamente cada biestable divide la frecuencia a la mitad y el periodo multiplica el doble, así que la idea es ir acoplando biestables hasta obtener la frecuencia deseada.

Laboratorio N°9

''Año de la lucha contra la corrupción y la impunidad".

Laboratorio N° 9

Circuitos Digitales

Contador Asincrono de 4 y 6 Etapas.

Alumno(s)		Nota
-Ccora Mamani, Jhair Antony
-Flores Zenteno, Hairo Alexis
-Neira Mamani, Pool Deivis
Grupo
Ciclo  2C5	Electrónica y Automatización – Circuitos Digitales
Fecha de entrega

Contadores síncronos

Los contadores síncronos suelen consistir en un elemento de memoria, que se implementa usando flip-flops y un elemento combinatorio, que es implementado tradicionalmente mediante puertas lógicas. Las puertas lógicas son circuitos lógicos con uno o más terminales de entrada y un terminal de salida, en el que la salida se conmuta entre dos niveles de tensión determinados por una combinación de señales de entrada. El uso de las puertas lógicas para la lógica combinacional suele reducir el costo de los componentes de los circuitos del contador a un mínimo absoluto, por lo que sigue siendo un enfoque popular.

Contadores asíncronos

Los contadores asíncronos, también conocidos como contadores de ondulación, son el tipo más simple, que requieren menos componentes y menos circuitería que contadores síncronos. Los contadores asíncronos son más fáciles de construir que sus contrapartes síncronas, pero la ausencia de un reloj interno también presenta varias desventajas importantes. Los flip-flops en un contador asíncrono cambia los estados en diferentes momentos, por lo que los retrasos en el cambio de un estado a otro, conocidos como retardos de propagación, se suman para crear un retardo global. Mientras más flip-flops contenga un contador asíncrono, mayor será el retardo global.

OBSERVACIONES Y CONCLUSIONES:

Al momento de la implementación del circuito del Laboratorio no hubo los cables suficientes, pero un compañero nos presto y se pudo completar el Laboratorio.

• Se identifico las aplicaciones de la Electrónica Digital.
• Se vieron algunos problemas de conexiones.
• Se vio el funcionamiento de las unidades y dispositivos de almacenamiento de información.
• Implementacion circuitos de lógica combinacional y secuencial.